Shear Stress - Shear Rate
Viscosity! If you ever think about it, what do you see?
Could it be you see thickness?
Thickness! You don’t have to understand much else. But understanding a few special things about it helps in everyday life. For example, heating something like pancake syrup makes it thinner and it flows better over the pancakes or waffles.
it thinner and it flows better over the pancakes or waffles.
However, if you are designing a new pancake syrup and its production process, it would be nice to know how it will respond to a range of different conditions.
I think I’d like to measure the syrup properties when it's warm, when it's cold, when it’s still, and when it’s moving. Like almost everything I try to understand about measurement, gauging viscosity characteristics turn out to be complicated.
To understand, let's start with some basic details about viscosity properties of liquids.
Viscosity is the force needed to move a liquid.
With most liquids, the faster you try to move it the harder it becomes.
That’s pretty simple.
You guessed it - that’s not how it goes all the time. Turns out there are different kinds of liquids and some do very strange things.
 Let’s start with the liquids I first talked about - faster/harder. They have a name for these. It is Newtonian. The faster you swish the water in the tub, the harder you have to swish. The viscosity formula is the difficulty of the swish divided by the speed of swishing.
Let’s start with the liquids I first talked about - faster/harder. They have a name for these. It is Newtonian. The faster you swish the water in the tub, the harder you have to swish. The viscosity formula is the difficulty of the swish divided by the speed of swishing.
The Other Liquids
The other kind of fluids has an array of bizarre properties.
Some get easier to move the faster you try to move them.
Some do not change until they reach a special speed.
Some are even stranger.
I bet you can guess what these spooky liquids are called - Non-Newtonian of course.
Key Viscosity Measurements
The two basic attributes of Viscosity Measurement are Shear Stress and Shear Rate. Shear Stress represents the force we discussed. Shear Rate relates to the speed of movement.
At this point, our viscosity definition related to swishing turns into a precise number. It is technically - Shear Stress divided by Shear Rate. For Newtonian fluids, this is the viscosity. For Non-Newtonian fluids, this is known as apparent viscosity.
Viscosity Shear Rate and Non-Newtonian Measurements
Non-Newtonian fluids present numerous conceptual and measurement problems.
Unlike simple liquids, where the relationship of speed and torque is constant for a given viscosity, Non-Newtonian Viscosity depends on changes in Shear Rate.
Getting a handle on the Shear Rate brings into play some complex dynamics.
The concept of liquid layers raises its head . Simple to write but a little bit hazy to visualize - layers in a homogeneous liquid?
. Simple to write but a little bit hazy to visualize - layers in a homogeneous liquid?
Two geometric elements are part of the formula that defines this shear rate. The area of the layers and the distance between the layers.
Who Cares About Viscosity Shear Rate in Non-Newtonian Fluids?
To see if we should proceed with this arcane analysis, maybe we sho uld look at who cares.
uld look at who cares.
When you assess the wide array of products and product functions that depend on the actions of a liquid, the importance of knowing viscosity becomes clear. A small sample of Non-Newtonian products include:
Mayonnaise Ketchup Pizza Dough Honey Yogurt
Taffy Paint Printers Ink Gels Nail Polish
Silly Putty Watery Sand Toothpaste Motor Oil Corn Starch
This partial list gives a window into the scope of who cares about Non-Newtonian fluids.
Looks like it’s worth going on?
Checking Out Non-Newtonian Liquids
Why do we need to go through all this complex analysis and measurement? Wouldn’t a simple spindle in the sample and different speeds get the answers we need for a Non-Newtonian liquid? That depends.
The simple approach can work for checking a process for QC standards over a narrow range of conditions.
However, if you are designing a system of pumps and piping to move a Non-Newtonian liquid, or have product characteristics that vary widely as conditions change, knowing the shear rate at different speeds is critical. For example, a pump with too much velocity, in a liquid that gets thicker the faster it goes (shear thickening), would clog valves.
For design, engineer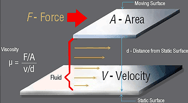 ing, and R&D, measurements of Non-Newtonian fluids need to produce comprehensive information on shear rate. Techniques that can portray the area of the layers and the distance between layers are needed to get measurements of apparent viscosities at different shear stress levels.
ing, and R&D, measurements of Non-Newtonian fluids need to produce comprehensive information on shear rate. Techniques that can portray the area of the layers and the distance between layers are needed to get measurements of apparent viscosities at different shear stress levels.
Rotational Viscometers and Shear Rate
The rotational viscometer is widely used to measure viscosity. It consists of a spindle or bob, which is placed in the liquid sample. This is attached to a drive that controls the rotational speed and which measures the torque needed to move the spindle. The speed relates to the Shear Rate and the torque relates to the Shear Stress.
To get the Viscosity of Newtonian liquids, this simple combination of speed and torque measurement is all that is needed.
The complexities of layer and layer separation come into play when working to 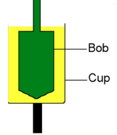 measure the apparent viscosity of Non-Newtonian fluids. The rotational viscometer system used for these measurements applies the Cup and Bob technique.
measure the apparent viscosity of Non-Newtonian fluids. The rotational viscometer system used for these measurements applies the Cup and Bob technique.
The surface area of the bob or spindle is known as, well, the surface area of the wall of the cup is set. These represent the areas of two liquid layers.
The distance between the spindle and the wall of the cup represents the distance between layers.
Using these two-layer areas and the layer separation, apparent viscosity can be calculated for Non-Newtonian liquids. The rotational speed represents the third element in the shear rate calculation.
The torque required to turn the spindle represents the shear stress.
The range of apparent Viscosity (shear stress/shear rate) can be determined by changing the speed/RPM of the spindle. This system is used for a wide scope of Non-Newtonian products.
Summary
Measuring viscosity is simple if you are interested in Newtonian products. Simply measure the RPM of a spindle and the torque required to make that speed happen. These translate into the shear stress /shear rate that is the formula for apparent viscosity.
Non-Newtonian products present more complex measurement problems because although the shear stress is measured in the same manner, the shear rate is no longer just the RPM of the spindle but takes into consideration the area of and distance between layers of the liquid.
As usual, every time I try to explain a simple concept I am confounded. It never turns out to be straightforward. 
If you find that this discourse might be useful or interesting to your associates, please share it.
Art
P.S. You can subscribe to our soliloquies, articles, and newsletters by placing your email address in the space to the right of the title.
P.P.S. See What Measures Shear Rate.

